無数の「金属比準結晶」を構成する方法を発見 パターンが少ないと思われていた準結晶の構造に新たな可能性
近畿大学(大阪府東大阪市)大学院総合理工学研究科 博士前期課程2年 中蔵 丈一郎および理工学部 教授 堂寺 知成、奈良女子大学(奈良県奈良市)理学部 教授 松澤 淳一、スロベニアのリュブリャナ大学ステファン研究所 教授 プリモシュ・ジハールらの研究チームは、原子や分子が規則正しく並ぶ結晶、規則性が無い非晶質とも異なる第3の固体「準結晶」の構造に関して、これまで少数しか知られていなかった準結晶タイリング※1 を無限に構成する方法を発見しました。人間が美しいと感じる比率と言われる金属比※2 の一種である「青銅比」の準結晶を平成29年(2017年)に近畿大学の研究チームが発見しており、今回、青銅比準結晶の考え方を応用し、その仲間の金属比準結晶を無限に構成できることを理論的に明らかにしました。
本研究成果により、金属ナノ粒子、酸化物フィルム、金属間化合物などの様々な複雑な物質構造を特徴付ける理論的枠組みを与えることが期待されます。
本研究成果は、令和元年(2019年)9月17日(火)に、英国科学誌「Nature Communications」にオンライン掲載されました。
【本件のポイント】
●「準結晶は珍しい」という常識を打ち破って、準結晶タイリングを無数に発見
●青銅比準結晶を親にした3の倍数の金属比を相似比にもつ準結晶タイリングを構成
●「普通の結晶は準結晶の成れの果て」というこれまでの常識とは逆転の発想を展開
【本件の内容】
準結晶は、原子や分子が一見バラバラなのに一定の規則性を持って並んでいるという特徴があります。これまでに金属比の一種である黄金比、白銀比、青銅比の構造が発見されていましたが、構造のパターンが非常に少ない物質だと思われてきました。
金属比は、x2-kx-1=0の解として求めることができ、k=1の時が黄金比、k=2の時が白銀比、k=3の時が青銅比となります。
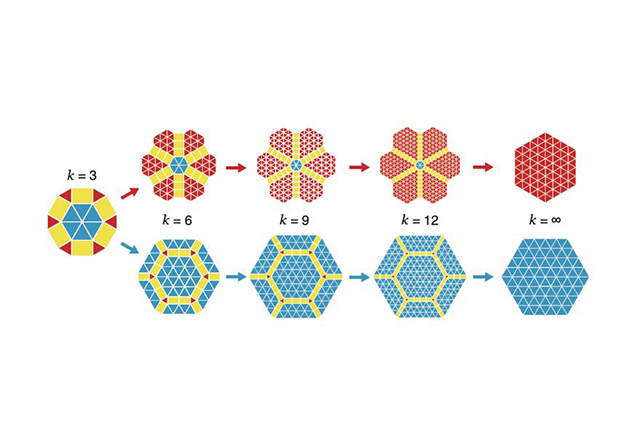
今回、青銅比の準結晶を構成する長方形および大きさの異なる2つの正三角形の3つの図形を用いて、長方形の長さの比率を変化させて準結晶タイリングのパターンを探ったところ、k=6の時、k=9の時、k=12の時…というように、3の倍数の時に準結晶となることがわかりました。
さらに、k=∞になると、正三角形だけで構成される規則正しく並んだ、結晶と同様の構造になります。
準結晶は、結晶や非晶質の例外的な物質だと思われていましたが、今回の研究により、無限に構造のパターンが存在し、その行き着く先が結晶であることを示しました。
今回の研究は、無数に準結晶構造が存在することを示しただけでなく、準結晶のタイリングが最終的に結晶と同様の構造となることを示したことで、これまでの常識を覆し、結晶科学の発展に大きく寄与するものです。
【研究の詳細】
古典結晶学で許されない回転対称性を持つShechtman、Steinhardtらの「準結晶」の発見は20世紀後半の物質科学上の大発見の1つに数えられ、平成23年(2011年)にShechtmanにノーベル賞が授与されました。それ以来、金属系以外の準結晶研究が爆発的に展開し、様々な準結晶がつぎつぎに明らかにされ、物質の種類、階層に関わらず普遍的に準結晶構造があることがわかってきました。金属物理学の一隅にあった準結晶研究は物理学、化学、ナノテクノロジーなど学問領域としても広がり、発見35年を経て新たな段階に入りつつあります。
こうした新しい準結晶構造の解明には、準結晶物質の少し前に発見された数学的タイリング理論が重要な役割を果たしました。1970年代にオックスフォード大学ペンローズ博士が発見した黄金比に基づく10回対称ペンローズタイリング、1980年代にかけて発見された白銀比に基づく8回対称アンマン・ビーンカータイリングなどの数学的タイリング理論です。準結晶構造は高次元の結晶とみなせるため、これらのタイリング理論から発生した結晶学は現在、高次元結晶学とよばれます。
本件では、近畿大学発祥の青銅比準結晶を親として、3の倍数の金属比の自己相似比をもつ準周期タイリングを無限に構成できることを示しました。大小の正三角形と長方形という3つの図形をさまざまに組み合わせ、長方形の長さの比率を調整することによって、自己相似な準結晶タイリングをいくらでも構成できることがわかりました。論文では2種類の金属比準結晶のタイリング理論と、その高次元結晶学、X線を当てた時にできる回折図形(フーリエ変換)の計算も示されます。
この新しい無数のタイリングは何の意味を持つのでしょうか。金属比の極限を取ると、準結晶タイリングは正三角形からなる六方格子(周期結晶)になります。そこから言えることは、準結晶は物珍しいのではなくて、むしろ沢山あって、そのなれの果てが通常の結晶とみなせます。この「準結晶の近似列の先に普通の結晶がある」という逆転の発想を専門用語で言い換えると、「近似準結晶」という言葉になります。すなわち、これまで知られていた「近似結晶」はローカルには準結晶に似ていますが、グローバルには周期結晶です。一方で、この論文で示された「近似準結晶」はローカルには周期結晶ですが、グローバルには準結晶です。お互いに相補的な関係と見なせます。
本研究によって、金属比準結晶、非金属比準結晶、整数比をもつ極限周期結晶、乱れたタイリング、不整合変調結晶を研究する包括的な枠組みが得られました。将来的には、例えば論文で議論した大きさの異なる正三角形、長方形などが現れる2つの長さスケールに特徴付けられるナノ粒子の自己集積であるとか、かなり単純なペアポテンシャルをもつ単分散な粒子に対して理論的に予言された双晶境界の超構造であるとか、非常に複雑な六方対称の構造に対して新しい展開が期待できます。
【掲載誌】
雑誌名:“Nature Communications”(インパクトファクター:11.878 2018)
※生物学、物理学、化学および地球科学のあらゆる領域における
高品質な研究を出版するオープンアクセスジャーナル
論文名:Metallic-mean quasicrystals as aperiodic approximants of periodic crystals
(周期結晶の近似準結晶としての「金属比準結晶」)
著 者:中蔵 丈一郎(近畿大学大学院 総合理工学研究科 理学専攻院生)、
プリモシュ・ジハール(スロベニア・リュブリャナ大学&ステファン研究所)、
松澤 淳一(奈良女子大学理学部)、堂寺 知成(近畿大学理工学部)
なお、本研究は、JSPS科研費(16H04037、19K03777)、JSPS二国間交流事業の助成のもとに行われました。
【用語解説】
※1 タイリング 三角形や四角形などの図形(タイル)の組み合わせで平面を隙間なく埋めること
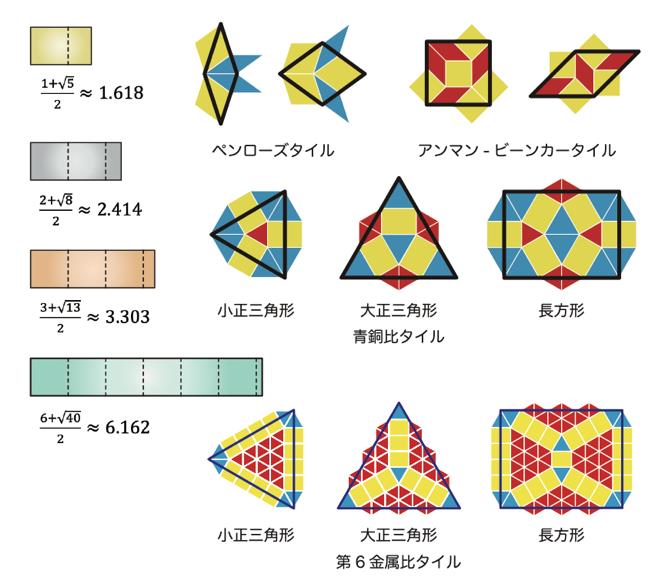
※2 金属比 x2-kx-1=0の正の解を金属比と言う。
下図は、1番目の金属比1.618(黄金比)の自己相似比をもつペンローズタイル、
2番目の金属比2.414(白銀比)の相似比をもつアンマン-ビーンカータイル、
3番目の金属比3.303(青銅比)をもつ青銅比タイル、
6番目の金属比6.162をもつ新タイルを示す。
黒枠タイルが色タイルの金属比倍になっている。
前2者と後2者の決定的違いは、タイルが2種類の辺の長さを持つということである。
【関連リンク】
理工学部 理学科 教授 堂寺 知成(ドウテラ トモナリ)
https://www.kindai.ac.jp/meikan/285-doutera-tomonari.html