フラストレートした量子磁性体の量子シミュレーション方法を提唱 –負の絶対温度をもつ気体の有効利用–
【概要】
一般的に「負(マイナス)の温度」と聞くと、冷凍庫の中(マイナス15℃程度)やドライアイス(マイナス78.5℃)などの寒い場所や冷たいものを想像するかもしれません。しかしながら、これらは摂氏温度に基づいて測ったから負になっているのであって、「絶対温度」に基づいて測定すると正(プラス)の温度をとります。絶対温度とは、摂氏温度で約マイナス273.15℃を絶対零度(0ケルビン)として測った温度のことです。絶対温度で測定すると、冷凍庫の中はプラス258ケルビン程度、ドライアイスはプラス195ケルビンになります。これらに限らず、私たちの身近にある通常の物質は正の絶対温度を持っています。では、物質の絶対温度を負にすることはできないのでしょうか?実は、実験室に超高真空(ultra high vacuum)状態を作り、レーザーや電磁石を使ってそこに非常に薄い原子気体(粒子数密度が大気の1万分の1程度)を閉じ込めて、慎重にその気体を操作すると、負の絶対温度を実現することができます。このように苦労して人工的に作り出した負の絶対温度の気体は何の役に立つのでしょうか?
青山学院大学理工学部(神奈川県相模原市)物理・数理学科山本 大輔助教、近畿大学理工学部(大阪府東大阪市)理学科物理学コース段下 一平准教授、理化学研究所創発物性科学研究センター(埼玉県和光市)福原 武ユニットリーダーは、この負温度の原子気体が、物性物理学における難題である「量子磁性体におけるフラストレーションの効果」を解明するためのシミュレータとして機能することを示しました。この成果は、「負の絶対温度」という基礎物理学的な概念が、量子デバイスにおける技術要素として大きな応用の可能性を持っていることを示唆します。
本件に関する論文は2020年3月20日にNature Researchの発行する学術雑誌”Communications Physics”に掲載されました。
【要点】
●負の絶対温度という特異な性質を量子シミュレータの機能として活用することを提案
●量子磁性体におけるフラストレーションの効果という物性物理学の難題の解決に道筋
●精密な数値計算から、量子シミュレーションの案内となる量子相転移点のベンチマークを作成
<論文掲載>
論文タイトル:Frustrated quantum magnetism with Bose gases in triangular optical lattices at negative absolute temperatures
掲載誌 :Communications Physics 3(2020)
著 者:山本 大輔助教(青山学院大学)、福原 武ユニットリーダー(理化学研究所)、
段下 一平准教授(近畿大学)
DOI :10.1038/s42005-020-0323-5
<本件の関連研究プロジェクト>
本研究は、科学技術振興機構(JST)戦略的創造研究推進事業CREST「量子状態の高度な制御に基づく革新的量子技術基盤の創出(研究総括:荒川 泰彦)」の研究課題「冷却原子の高度制御に基づく革新的光格子量子シミュレーター開発(研究代表者:高橋 義朗)」、文部科学省 光・量子飛躍フラッグシッププログラム(Q-LEAP)量子情報処理技術領域の基礎基盤研究「アト秒ナノメートル領域の時空間光制御に基づく冷却原子量子シミュレータの開発と量子計算への応用(研究代表者:大森 賢治)JPMXS0118069021」、内閣府革新的研究開発推進プログラム(ImPACT)「量子人工脳を量子ネットワークでつなぐ高度知識社会基盤の実現(プログラム・マネージャー:山本 喜久)」、日本学術振興会(JSPS)科学研究費助成事業基盤研究S「光格子中超低温原子気体の軌道及びスピン自由度を駆使した新量子物性の開拓(研究代表者:高橋 義朗)」、科学研究費助成事業基盤研究C「固体物質系と光格子量子シミュレータを繋ぐ新奇フラストレート量子物性の理論研究(研究代表者:山本 大輔)」、科学研究費助成事業基盤研究C「フラットバンドを持つ光格子を用いた新奇超伝導物性の開拓(研究代表者:土屋 俊二)」、科学研究費助成事業基盤研究B「カゴメ格子量子気体顕微鏡による量子スピン液体の研究(研究代表者:福原 武)」、科学研究費助成事業基盤研究C「ホログラフィー原理と光格子中の冷却気体の協奏による量子重力実現の提案(研究代表者:段下 一平)」による支援を受けて行われました。
<背景>
私たち現代人の生活になくてはならないスマートフォンやパソコンの便利な機能の多くは、固体材料のなかにある無数の電子をうまくあやつることで実現されています。より便利な機能を生み出していく上で、電子の集団について理解を深めていくことがとても重要です。電子の集団について語る上で欠かせないことは、電子一つ一つが量子力学というミクロの世界の法則に従っていて、私たちのようなマクロな世界の住民からするととても奇妙にみえる性質を持っているということです。例えば、マクロな物体であるビリヤードの玉を考えると、秒速1メートルで打ち出した玉の1秒後における玉の位置は決まっています。対照的に、同じ速度で真空中に電子が打ち出された場合、1秒後の電子の位置は決まりません。つまり、同じ条件の実験を繰り返すと、測定するたびに電子の位置が変わるのです。
半導体や磁石のような固体材料のなかの電子集団のように、量子力学に従う「小さなつぶ」が多数集まり、互いに相互作用している物質は量子多体系とよばれます。つぶの数が多いために、物理学の伝統技法である手計算だけではこれら量子多体系を正確に理解することができないので、計算機を用いた数値シミュレーションが研究の主要なアプローチです。しかしながら、古典計算機を用いると系を大きくするにつれて計算量が膨大になってしまうため、現実の物質と比較できるサイズの量子多体系で数値シミュレーションをする一般的な手法は現在のところ存在しません。つまり、「電子機器のさらなる機能向上のために、固体中の電子集団について理解を深めよう」というのはお題目としてはわかりやすいのですが、実際にやろうとするととても難しい問題なのです。
この困難を回避する方法論として、量子シミュレーションが近年注目を集めています。量子シミュレーションとは、物質中で起きる複雑な物理現象を人工的に作成した制御性の高い別のシステムを使ってシミュレーションすることを意味しています。これだけだととても難しいことのように聞こえますが、この類の「シミュレーション」の身近な例として、住宅などの建築物の耐震性を調べるために実施する地震シミュレーション(過去の巨大地震の地震波を実験室で再現して、その地震波で建築物を揺らす)を想像してもらうとわかりやすいかもしれません。地震シミュレーションでは建築物と地震波という古典力学に従うものを実験室で再現しているのに対して、量子シミュレーションでは固体中の電子集団という量子力学に従うものを再現します。
近年、極低温の希薄な原子気体を、レーザー光を組み合わせてできる光格子という人工的な結晶格子構造の中に閉じ込めることで、金属中の電子と類似した量子多体系を実現し、その性質を明らかにしようとする実験が注目を集めています。光格子はレーザー光で作成された山と谷を周期的に繰り返す格子構造を持ち、この状況は固体中で正電荷を持つイオンが周期的に並んで結晶になっている状況と似ています。したがって、図1で示すように、ナノケルビン(1ナノケルビンは1ケルビンの10億分の1の温度。これは地球上で実現される最も低い温度である。)程度まで冷却された原子気体を光格子の中に閉じ込めることで、あたかも電子が固体物質の中を動き回るような状況を作ることができます。このようにして原子気体で固体中の電子を模倣し、磁性や電気伝導や量子相転移などの興味深い現象をシミュレーションすることで、固体物質の性質を深く理解することができるのです。
<研究の経緯>
量子多体系の中でも特に理論的な解析が困難なものとして、フラストレートした量子磁性体が知られています。フラストレートした量子磁性体とは、幾何学的配置や逆の効果をもつ相互作用の競合によって、電子のスピン※1 間に働く全ての相互作用エネルギーを最小にすることができない状況をいいます。自然界は絶対零度の平衡状態においてエネルギーが最小の状態を好みますが、それを決めることが難しいため自然はフラストレーションを感じることになります。一般に、フラストレートした磁性体では最も安定する状態が複数存在しますが、絶対零度では一つの状態が選ばれます。このとき思いもよらぬ状態が選ばれることがあり、これが新しい現象の発見につながる場合があります。
具体例として、図2のような三角形を基調とした格子構造を持つ磁性体を考えます。格子点にある矢印はそこに局在した電子のスピンの向きを表します。隣同士のスピンに反強磁性的な相互作用が働くとすると、低温の平衡状態において格子点AとBのスピンは互いに反対方向を向くことでエネルギーを下げようとします。しかしながら、そうなると格子点Cのスピンは上を向けばBのスピンとの相互作用エネルギーを損してしまうし、下を向けばAのスピンとの相互作用エネルギーを損してしまい、エネルギー最小の配置が決まりません。このフラストレーションと量子力学的な不確定性を併せ持つ量子磁性体では、スピン液体状態※2 やゆらぎによる秩序化※3 といった特異な性質が現れることが知られています。しかしながら、理論的な解析の困難さのために、これらの興味深い物性を系統的に理解できない状況が長年続いています。そのため、フラストレートした量子磁性体を精密に解析できる数少ない手段として、この系の量子シミュレーション研究の発展が強く望まれています。
<研究成果>
そこで本研究では、光格子中の原子気体を用いてフラストレートした量子磁性体を量子シミュレーションするための方法を提唱しました。今回の方法で鍵となる要素が「負の絶対温度」です。絶対温度とは、目盛り幅は摂氏温度と同じにしたまま、摂氏温度で約マイナス273.15℃を絶対零度(0ケルビン)として測った温度のことです。通常我々の身の回りにある物質は正の絶対温度をとります。この理由は単純で、その名称から素朴に連想されるのとは対照的に、負の絶対温度を持つ物質はいかなる正の絶対温度の物質よりも熱いからです。つまり、負の絶対温度の物質をなんとかして作ったとしても、通常は周りにある正の絶対温度の物質(環境と呼ばれる)に熱を放出して、正の絶対温度に落ち着いてしまうのです。しかしながら、光格子中の原子気体は、図3aのように、光トラップ※4 や磁気トラップ※5 によって超高真空中に閉じ込めて作成されるため、環境から孤立していて熱を放出しません。この性質を生かして、2013年にルートヴィヒ・マクシミリアン大学ミュンヘン(ドイツ)のグループが光格子中のボース気体(ボース統計性※6 を持つ原子からなる気体)における安定な負温度状態を実現しています。
ボース気体を用いて磁性体を量子シミュレーションするためのもう一つの鍵は「物質波の位相」です。原子などのミクロな粒子の実態は「物質波」と呼ばれる波動です。この物質波は、音波や電磁波などの身近な波と同様に、波動関数※7 として表されます。しかしながら、図3aとbで示すように、身近な波の波動関数の値が実数であるのとは違い、物質波の波動関数の値は複素数です。一つの複素数は実部と虚部と呼ばれる二つの実数によって決まります。したがって、図3cのように、複素数は実部をx軸、虚部をy軸にとった二次元平面(複素平面と呼ばれる)の上の点として表すことができます。複素数の「位相」とは原点(0,0)からこの点を見たときの向きを、角度で表したものです。直感に訴えるために、x軸方向を東、y軸方向を北と呼びます。もし、原点から見てこの点が真東にあるなら位相は0°です。原点から見てこの点が北にあるなら90°、西なら180°、南なら270°、北東なら45°・・・という具合です。光格子の各格子点にあるボース気体の波動関数はそれぞれが一つの複素数であるため位相を持っています。これが物質波の位相です。これを磁性体中の電子スピンに見立てることが、ボース気体を用いて磁性体を模倣する常套手段です。
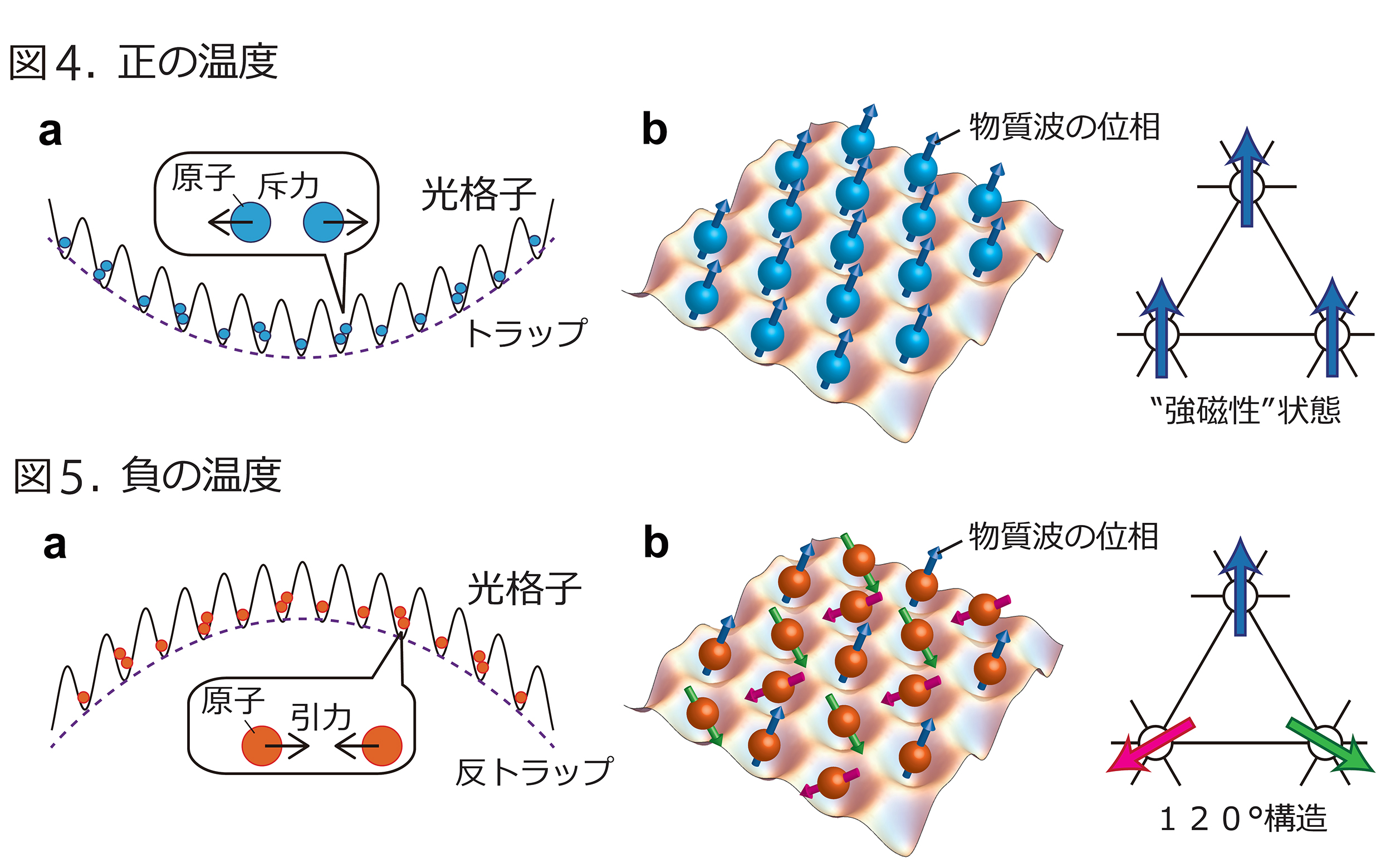
本研究では、まず三角形の格子構造を持つ光格子の中で負温度のボース気体を作る具体的な方法を示しました。対比のために、まず正の絶対温度で低温の気体の場合を説明しておくと、図4aのように、原子同士が互いに反発し、電場や磁場を組み合わせて原子を捕捉するお椀のような形状のトラップポテンシャルの底に溜まっている状態が安定な配置となります。また、ボース気体の位相は全ての格子点で揃い、これは磁性体でいう強磁性状態(磁石)にあたります(図4b)。それとは対照的に、負の絶対温度でかつ絶対零度に近い温度の場合、原子同士が互いに引き合い、トラップポテンシャルの頂上付近に位置するという通常のボース気体が不安定化する状況で安定化します(図5a)。さらに、ボース気体の位相が図5bのような120°構造※8 をとることから、当該系がフラストレーションを持っていることがわかります。続いて、三角光格子を深くしていくことで、量子ゆらぎを増大させ、超流動相から絶縁体相への量子相転移※9 が引き起こされることを示しました。精密な計算機シミュレーションを用いて、量子ゆらぎとフラストレーションの複合効果でこの量子相転移の転移点が大きく変化することを明らかにしました。ここで決めた転移点は、将来の量子シミュレーション実験に対するベンチマークとしてとても有用です。
<今後の展開>
本研究の提案が将来の量子シミュレーション実験で実現されれば、量子磁性体におけるフラストレーションの効果という物性物理学における難問を解決する糸口になると期待されます。また、本研究によって、負の絶対温度という基礎物理学的な概念の量子シミュレータの高機能化における有用性が示されたことも特筆すべき点です。近年、量子シミュレータに利用できるほどの制御性をもつ量子プラットフォームが急速に増えてきており、負温度という概念の応用がこれらの量子デバイス開発に新たな潮流を生む可能性があります。
【用語解説】
※1 電子のスピン・・・電子の自転運動に対応する物理量。自転の向きに右ねじを回したとき、ねじの進む向きがスピンの向きである。電子は負の電荷をもつので、自身の自転によって小さな磁石の性質(磁気モーメント)をもつ。スピンは量子力学の法則(不確定性原理)に従うので、スピンの向きを完全に決定することはできない。
※2 スピン液体状態・・・水が氷になるように、スピンの集団も液体や固体といった異なる状態を取り得る。水のような通常の液体は、熱による粒子のランダムな運動(熱ゆらぎ)によって流動的な性質を示す。一方でスピンの液体状態とは、極低温での量子力学の不確定性原理に起因したゆらぎ(量子ゆらぎ)によって引き起こされる不思議な液体状態である。
※3 ゆらぎによる秩序化・・・物質を低温に冷やしていくと、通常は内部の粒子はなんらかの「秩序」を持つ。例えば強磁性体(磁石)の中では、無数の電子のスピンが同じ方向に揃って向く秩序を持つことでマクロな磁石としての性質が現れる。物質の温度が上昇すると、熱によるゆらぎが起こり、そのような秩序は壊れてしまう。しかし、エネルギー最小の配置(秩序)が簡単には決まらないフラストレートした量子磁性体では、むしろ量子力学的なゆらぎが粒子の秩序を作り出すという逆の現象が起こり得る。
※4 光トラップ・・・原子の共鳴周波数よりも少し小さい周波数を持つレーザー光は、原子を引きつける。この性質を利用すると、レーザー光を集光して原子を空間の狭い領域に閉じ込めることができる。
※5 磁気トラップ・・・ナトリウムやルビジウムなどのアルカリ金属原子は一つ一つが小さな磁石として振る舞うため、空間中に磁場の強い場所を作ることでそこに原子を引きつけて閉じ込めることができる。
※6 ボース統計性・・・粒子を大きく2種類に分類するとフェルミ粒子とボース粒子に分けられる。例えば電子はフェルミ粒子であり、光子はボース粒子である。複数の電子や陽子、中性子から構成される原子も、それぞれの構成個数によってフェルミ粒子になるかボース粒子になるかが決まっている。このうちボース粒子は、複数の粒子がある一つの量子状態を同時に占めることが可能であるという統計的な性質を持つ。
※7 波動関数・・・波動を特徴付ける物理量を位置と時間の関数として表したもの。例えば、空気中の音波であれば空気の密度、電磁波であれば電場と磁場が波動関数となる。
※8 120°構造・・・図2に示すように格子点A、B、Cのスピンの向きを互いに反対を向かせることが不可能な場合、それぞれの相対角を120°ずつ傾けることでなるべく反強磁性相互作用を得しようとするスピン配置が現れる。そのような配置を120°構造と呼ぶ(図4b参照)。
※9 量子相転移・・・例えば氷を温めると水に変化するような現象を一般に相転移という。通常の相転移現象は、温度の変化に伴う熱ゆらぎによって引き起こされる。一方で量子力学的な性質の強い物質では、たとえ絶対零度付近であっても量子力学的なゆらぎによって相転移現象が誘起され得る。
【関連リンク】
理工学部 理学科 准教授 段下 一平(ダンシタ イッペイ)
https://www.kindai.ac.jp/meikan/2161-danshita-ippei.html